
電子回路を勉強していく中で「RLC直列回路の過渡現象」がよく出てくる。
なぜ過渡現象が起きるの?
こんな疑問を解消します。
RLC直列回路の過渡現象は、電子回路では発生することが多いため、必ず理解しておくべきです。
そこで今回は、『RLC直列回路の過渡現象』について解説します!
・ 電圧の関係式
・ 微分方程式の解法
・ RLC直列回路の電流波形
・ RLC直列回路の電圧波形
・ シミュレーションでの確認①
・ シミュレーションでの確認②
・ RLC直列回路を直観的に理解できない場合
・ シミュレーションソフト『LTspice』
★【2023最新版】回路設計の年収は?現役エンジニアが解説します!
困っている人 回路設計に興味がある。 年収はどれくらいなの? こんな疑問を解消します。 回路設計エンジニアは『経験を積めば1,000万円も狙える職業』です。 トヨタ自動車やキーエンスなど、多[…]
RLC直列回路の構成
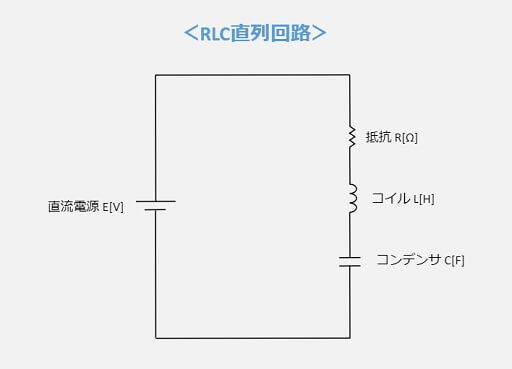
RLC直列回路とは、『抵抗・コイル・コンデンサが直列に接続された回路』です。
RLCについては、以下の由来があります。
【RLCの意味】
R:Resistor(抵抗)の頭文字
L:Coil(コイル)の最後の文字
C:Capacitande(コンデンサ)の頭文字

このRLC回路について、まずは電流を導出してみましょう。
電圧の関係式
キルヒホッフの第2法則を用いると『電圧の関係式』は下記のようになります。
$$ Vr + Vl + Vc = E $$
$$⇔ RI + L\frac{dI}{dt} + \frac{1}{C}\int Idt = E $$
\(I \):回路に流れる電流
\(E \):直流電源の電圧
\( Vr \) :抵抗の電位差
\( Vl \):コイルの電位差
\( Vc \):コンデンサの電位差
この微分方程式を解けば、『回路に流れる電流』を導出できるのです。

微分方程式の解き方も併せて、丁寧に解説していきます。
微分方程式の解法

微分方程式の解法は、下記となります。
$$ y^{\prime\prime} + ay^{\prime} + by = 0 ・・・①$$
①の一般解は、下記方程式の解を用いて表すことができる。
$$ γ^2 + aγ + b = 0 ・・・②$$
1.②が異なる2つの実数解(p,q)を持つとき、
$$ y = Se^{px} + Te^{qx} $$
2.②が異なる2つの虚数解(h±ki)を持つとき、
$$ y = e^{hx}(Scoskx+ Tsinkx) $$
3.②が異なる重解(p)を持つとき、
$$ y = e^{px}(S+ Tx) $$
$$※S,Tは定数$$

覚える必要はなく、このような解き方があることを知っておくだけで良いです。
RLC直列回路の電流波形
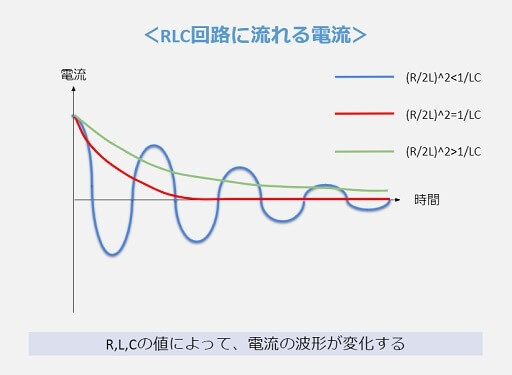
上図のように、R,L,Cの値によって『電流の波形』が異なります。
では、微分方程式を解いて、電流を導出していきましょう。
$$ RI + L\frac{dI}{dt} + \frac{1}{C}\int Idt = E ・・・①$$
①の両辺をtで微分すると、
$$ R\frac{dI}{dt} + L\frac{d^2I}{dt^2} + \frac{1}{C} = 0 ・・・②$$
②の微分方程式を解きやすいように両辺をLで割って並び替えると、
$$ \frac{d^2I}{dt^2} + \frac{R}{L}\frac{dI}{dt} + \frac{1}{LC} = 0 ・・・③$$
③の解は、下記方程式④の解を用いて表すことができる。
$$ γ^2 + \frac{R}{L}γ + \frac{1}{LC} = 0 ・・・④$$
解の公式を用いて④を解くと、
$$ γ = -\frac{R}{2L} \pm\sqrt{\left(\frac{R}{2L}\right)^2-\frac{1}{LC}} $$
1.④が異なる2つの実数解を持つとき、\( \left(\frac{R}{2L}\right)^2>\frac{1}{LC} \)であり、
\begin{eqnarray}
I = &S&e^{\left(-\frac{R}{2L} +\sqrt{\left(\frac{R}{2L}\right)^2-\frac{1}{LC}}\right)t} \\
&+& Te^{\left(-\frac{R}{2L} -\sqrt{\left(\frac{R}{2L}\right)^2-\frac{1}{LC}}\right)t}
\end{eqnarray}
2.②が異なる2つの虚数解を持つとき、\( \left(\frac{R}{2L}\right)^2<\frac{1}{LC} \)であり、 \begin{eqnarray} y = &e&^{(-\frac{R}{2L})t}(Scos\left(\sqrt{\frac{1}{LC}-\left(\frac{R}{2L}\right)^2}\right)t \\ &+& Tsin\left(\sqrt{\frac{1}{LC}-\left(\frac{R}{2L}\right)^2}\right)t) \end{eqnarray} 3.②が異なる重解を持つとき、\( \left(\frac{R}{2L}\right)^2=\frac{1}{LC} \)であり、 $$ y = e^{\left(-\frac{R}{2L}\right)t}(S+ Tt) $$ $$ ※S,Tは定数 $$

どの場合にも、電流は次第に流れなくなることが分かります。
RLC直列回路の電圧波形
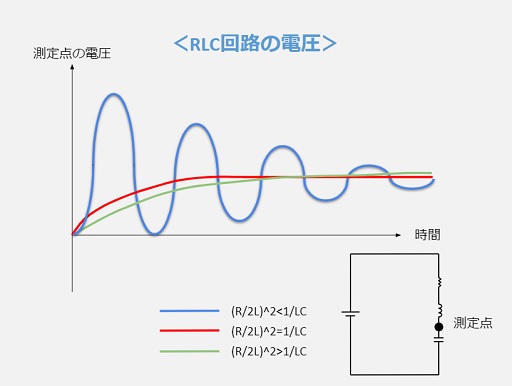
R,L,Cの値によって、測定点の電圧波形は、上図のようになります。
1. \( \left(\frac{R}{2L}\right)^2 \) > \( \frac{1}{LC} \)
電流はゆっくりと流れなくなるため、測定点の電圧はゆっくりと電源電圧に近づいていきます。
2. \( \left(\frac{R}{2L}\right)^2\) < \( \frac{1}{LC} \)
\( Vc = \frac{1}{C}\int Idt \)であるため、測定点の電圧は、電流と\( \frac{π}{2} \)ずれた波形になります。
最後には電流が流れなくなるため、測定点の電圧は電源電圧と同じになります。
3. \( \left(\frac{R}{2L}\right)^2\) = \( \frac{1}{LC} \)
1と同様に、電流はゆっくりと流れなくなるため、測定点の電圧はゆっくりと電源電圧に近づいていきます。

電流波形を理解しておけば、電圧波形も理解できるのです。
シミュレーションでの確認①
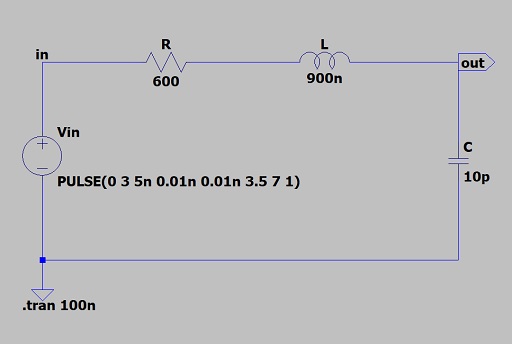
上図のような回路について、シミュレーションで実際の波形を確認してみましょう。
各素子の定数は、以下のように設定してあります。
【定数の設定】
抵抗R:600Ω
インダクタンスL:900nH
コンデンサC:10pF
電源電圧E:3V
この時、電流波形・電圧波形は以下のように導出できます。
【電流波形・電圧波形の導出】
\( \left(\frac{R}{2L}\right)^2 = \left(\frac{600}{2×900n}\right)^2 = \frac{1}{9}×10^{18} \)
\( \frac{1}{LC} = \frac{1}{900n×10p} = \frac{1}{9}×10^{18} \)
\( \left(\frac{R}{2L}\right)^2 = \frac{1}{LC} \)より、電流波形:減少、電圧波形:上昇となります。
シミュレーション結果は、以下のようになりました。
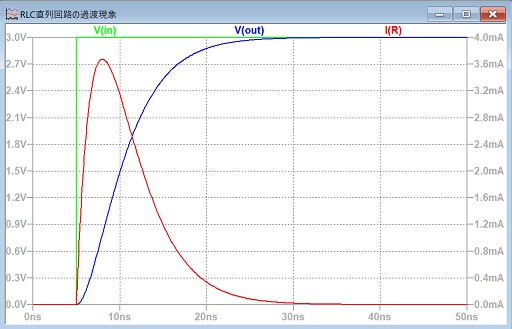

机上で導出した通りの波形となりましたね。
シミュレーションでの確認②
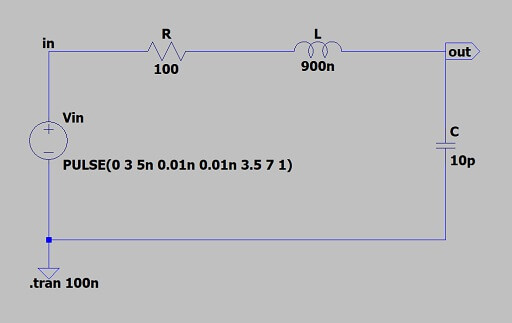
抵抗を小さくして、シミュレーションで実際の波形を確認してみましょう。
各素子の定数は、以下のように設定してあります。
【定数の設定】
抵抗R:600Ω ⇒ 100Ω
インダクタンスL:900nH
コンデンサC:10pF
電源電圧E:3V
この時、電流波形・電圧波形は以下のように導出できます。
【電流波形・電圧波形の導出】
\( \left(\frac{R}{2L}\right)^2 = \left(\frac{100}{2×900n}\right)^2 = \frac{1}{324}×10^{18} \)
\( \frac{1}{LC} = \frac{1}{900n×10p} = \frac{1}{9}×10^{18} \)
\( \left(\frac{R}{2L}\right)^2 < \frac{1}{LC} \)より、電流波形:振動、電圧波形:振動となります。
シミュレーション結果は、以下のようになりました。
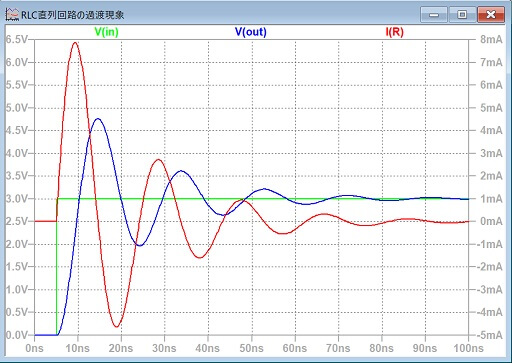

入力電圧に対して、出力電圧の最大値がかなり大きくなっていますね。
RLC直列回路を直観的に理解できない場合

RLC直列回路を直観的に理解できない場合、先に下記2つを理解することをオススメします。
・RC回路
・CR回路
上記2つは、『回路設計する上で必須の基礎知識』です。

怪しいなと思った方は、ぜひ下記をご覧ください。
困っている人 電子回路を勉強していく中で「RC回路」がよく出てくるけど、理屈が分からない。 どんな原理なんだろう? こんな疑問を解消します。 電子回路の基本となる「RC回路」は、実際の回路でもよく使用されてい[…]
困っている人 電子回路を勉強していく中で「CR回路」がよく出てくるけど、理屈が分からない。 どんな原理なんだろう? こんな疑問を解消します。 CR回路は、『ハイパスフィルタとして使用されることが多い回路』です[…]
シミュレーションソフト『LTspice』

今回記事で登場しているシミュレーションは、LTspiceを使用しています。
フリーソフトであるため、『誰でも無料で利用可能』です。

興味がある方は、下記の書籍を参考にして、ぜひ利用してみて下さい。
★【2023最新版】LTspiceのオススメ本 10選 を紹介します!
困っている人 LTspiceの使い方をマスターしたい。 オススメの本ってどれ? こんな要望に応えます。 これからLTspice使用を検討している方の中には、『どうやって使い方を学ぶべきか悩んでいる方』も多いと[…]
RLC直列回路の過渡現象まとめ

いかがでしたでしょうか。
電子回路を設計する上で『RLC直列回路の過渡現象』は必須の知識です。
RLC直列回路の過渡現象をしっかりと理解しましょう。
この記事が、皆様のお役に立てば幸いです。
\現役の回路設計エンジニアが解説!/
人気記事 【2023最新版】回路設計の年収は?現役エンジニアが解説します!
人気記事 【2023最新版】電子回路でオススメの本 7選を紹介します!






